Простые числа и решето Эратосфена

Век живи — век учись (и дураком помрёшь). Казалось бы, чем могут меня, взрослую тётку, удивить школьные учебники дочери? Это всего лишь пятый класс, последний класс начальной школы. Все мы там были и все учились чему-нибудь и как-нибудь. А если что и забыли, то Гугль всемогущий непременно напомнит. Но нет, есть, оказывается, темы и информация, от которой глаза сворачиваются бубликом, после чего лезут на лоб, причём прямо в такой позе. Дошла моя деточка до темы простых и составных чисел.

Тема простая и особых трудностей не вызывающая: это всего лишь числа, которые делятся на единицу и сами на себя — и больше ни на что. Любой знакомый с таблицей умножения ребёнок методом подбора способен выяснить, простое это число или нет: достаточно просто выяснить, на что делится то или иное число: 2 делится на 2 и 1 и больше ни на что. Оно «простое, как мычание». 4 же делится на 2, на 1, а ещё на 4. Значит, сие число у нас «не мычит». Казалось бы, на этом тему можно бы закрыть. Но нет! Эратосфен, царствие ему небесное, подложил детям баааальшую свинью, придумав свой метод решета (а учёные умы современности решили детский кругозор расширить и внесли его в детские учебники), который позволяет определить все простые числа в ряду до 100, последовательно вычёркивая те, которые простыми не являются. Для этого надо всего лишь последовательно вычеркнуть из таблицы все числа, кратные двум, затем кратные трём, затем кратные пяти и наконец семи, то есть несколько раз «просеять» числа таблицы, определив для каждой, делится ли оно на каждое из нужных нам чисел. Те числа, которые останутся в живых после этой зачистки, и являются простыми. Задача всего лишь на таблицу умножения, но, взявшись за дело, в какой-то момент понимаешь, что она как-то подозрительно похожа на тот из подвигов Геракла, который был самым вонючим неблагодарным (Авгиевы конюшни, если кто вдруг не помнит). Попробуйте и убедитесь сами, что развлечение это так себе… 🙂

Не знаю, до какого числа и на какой кратности вы дошли. Но вы сейчас занялись тем, что своей дочери делать я настоятельно не рекомендовала. Если есть такое большое желание поупражняться в умножении-делении, прокачать навыки быстрого устного счёта — на то у нас, слава Богу, есть небезызвестный Кумон. Здесь задача не в том, кто быстрее и точнее проделит все числа, нигде не заблудившись и ничего не перепутав. Мы все, конечно, живые компьютеры, но нам не нужно оценивать «производительность компьютера имярек» (подставить имя собственного ребёнка) таким варварским методом. Нужно просто найти простые числа и желательно это сделать наименее трудозатратным для ребёнка способом. 🙂 Если остановиться и немного подумать, то можно найти какой-нибудь лайфхак.

Начнём с кратности двум. Что есть числа, кратные двум? Это числа чётные. 2, 4, 6, 8… При этом, как мы помним, 2 — делится только на 1 и на саму себя. Поэтому её не трогаем, а остальные чётные обводим (или закрашиваем) каким-нибудь одним цветом. Ребёнок решил не мелочиться и просто прорисовать дорожки. 🙂

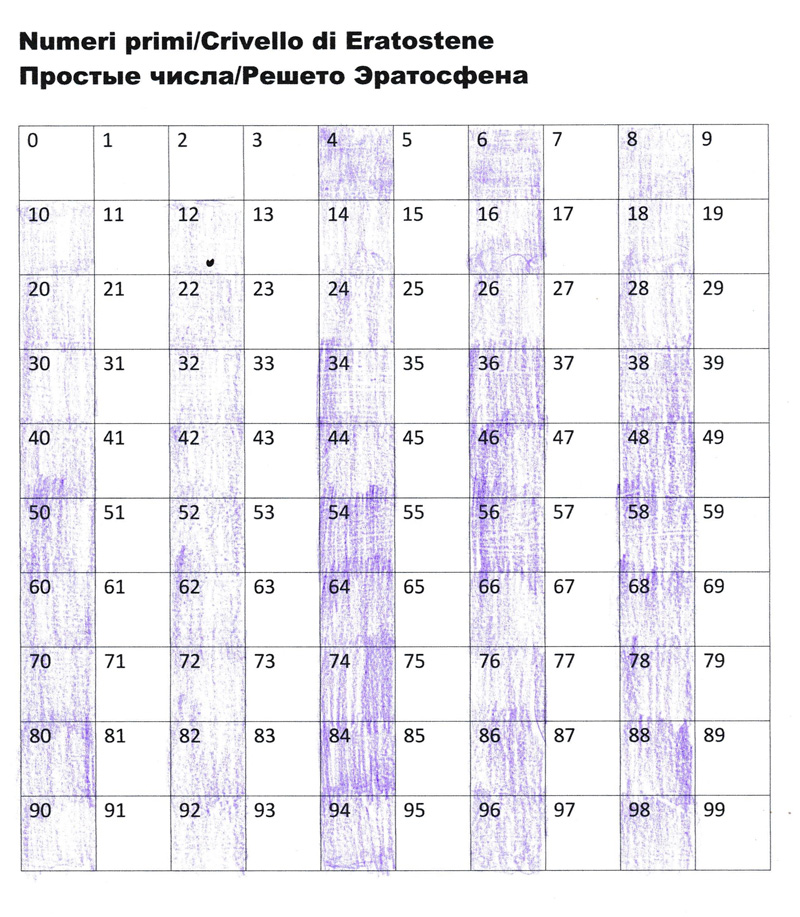
Как видим, наше решето сразу порядком опустело. И это отличная новость. 🙂 Теперь можно переходить к цифре 3. Берём карандаш (ручку, фломастер) другого цвета и подбираемся к цифре 3, у которой тоже дипломатический иммунитет (делится только на саму себя и на 1), так что трогать её нельзя. Ближайшая кратная трём будет 6. За ней 9. За ней 12. Вы ничего не заметили? Мы с вами сейчас двигаемся в ритме вальса, друзья. Раз-два-три, раз-два-три, раз-два-три… Уже поняли, на какой такт ставить свою цветную отметку? Прекрасно!

Включайте хронометр и засекайте, сколько времени и при каком расходе нервов у ваших цветов жизни ушло на уничтожение союзников цифры 3, а за ними по тому же самому принципу (дипломатический иммунитет и размер шага) — и двух других вражеских лагерей (пятёрочников и семёрочников) — я надеюсь, вы сами уже догадались, что (какой ритм) и от какой цифры нужно стучать. 🙂

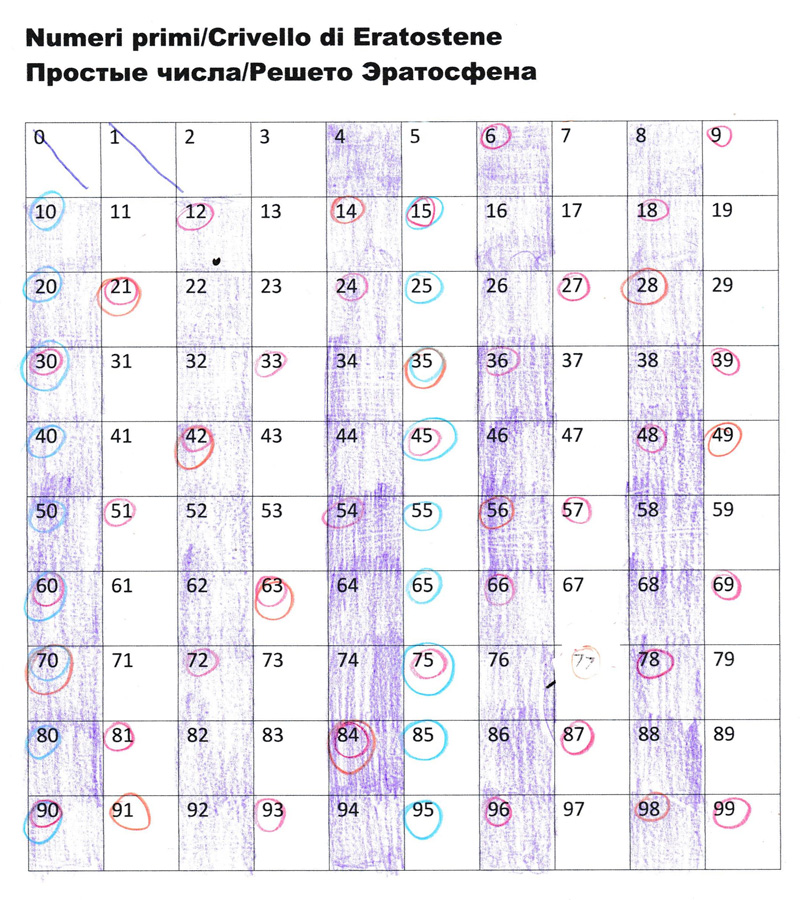
Ноль и один не являются простыми числами, они просто наблюдатели. 🙂 Их присутствие здесь полезно по сути одной-единственной причине: они придают табличке симметричность. Поэтому мы их зачёркиваем, чтоб они нас не путали. А вот все остальные незакрашенные числа как раз и являются теми самыми простыми числами, которые ребёнку нужно было выявить. «Элементарно, Ватсон!»
Ребёнку настолько понравилась игра в раскраску и отстукивание ритма, что она повторила её на бис, два раза подряд. 🙂

P.S. Математики ещё не нашли все существующие простые чиса. Но с помощью мощных компьютеров и алгоритмов добрались до чисел, состоящих из 23 миллионов цифр. Наверняка кто-то из сегодняшних детей, сейчас мучающихся (или наоборот забавляющихся) с эрастофеновым решетом, однажды зайдёт ещё дальше в этом квесте. А кто-то будет составлять учебники для новых поколений детишек, добавляя туда новые материалы… Пожелаем терпения тем новым поколениям детей и их родителям. Мы, ваши предки, всей душой с вами. 😀

Visits: 13